C: Calcul du débit de sortie d'un
réseau fluvial
Un réseau
fluvial peut être représenté par un arbre plan (les feuilles représentant les
sources de toutes les rivières du réseau et les nœuds internes les jonctions de
plusieurs rivières). Le but de ce problème est de calculer le débit de sortie
d’un tel réseau, étant donnée une description de la topologie du réseau (de
l'arbre), en appliquant le principe suivant :
- le débit de sortie est le débit à la
racine de l'arbre,
- les sources ont un débit de 1,
- à une jonction donnée, si le débit maximum
arrivant en cette jonction est D et que M rivières arrivant en cette
jonction ont ce débit D, alors le débit de la rivière issue de cette
jonction est égal à D+M-1.
Entrée
L'entrée du problème sera
constituée de nombres décrivant la topologie d'un arbre (réseau fluvial) aux
sommets étiquetés (par un parcours en profondeur par exemple). Cette
description prend la forme suivante : un entier indiquant le nombre N de
sommets, suivi de N paires d'entiers décrivant les arêtes de l'arbre (la paire
i j indique que le sommet étiqueté i est un des enfants du sommet étiqueté j. On
suppose que l'entré est correcte et décrit bien un arbre. On impose de plus que
ces 2N-1 nombres soient entrés en un seule ligne se terminant par un retour
chariot avec un seul espace entre deux nombres, aucun espace superflu au début
ou à la fin de la ligne.
Sortie
La sortie attendue est le
débit de sortie du réseau fluvial : il s'agit donc d'un nombre entier, sans
espace superflu avant ou après, suivi d'un retour chariot.
Exemple
Voici par
exemple un exemple d'arbre à 10 sommets.
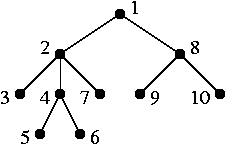
Exemple d'entrée
On peut décrire cet arbre
par la liste suivante d'entiers.
10 5 4 9 8 2 1 6 4 3 2 10 8 4 2 7 2 8 1
Exemple de sortie
La sortie attendue est 3 :
- les sommets 3, 5, 6, 7, 9, 10 sont des
feuilles et les rivières qui en sont issues ont débit 1;
- les deux fils du sommet 4 on débit 1 et ce
sommet a donc débit 2 (il en est de même pour le sommet 8);
- les trois fils du sommet 2 ont comme
débits 1, 2, 1, le maximum est 2 et une seule rivière a ce débit, ce
sommet a donc comme débit 2 (2 + 1 - 1);
- les deux fils de la racine 1 ont un débit
de 2 et le réseau fluvial a donc un débit de sortie de 3 (2 + 2 –1).