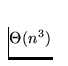 .
. et g est
et g est 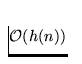 , alors
f est
, alors
f est 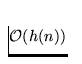 .
.
Automne 1998
Automne 1998
type arbre ::= Feuille nat | Noeud nat arbre arbreDans de tels arbres, tant les feuilles que les noeuds internes conservent de l'information (nombre naturel).
Définissons aussi quelques opérations sur ds tels arbres:
infos :: arbre -> sequence{nat}
infos(Feuille n) = [n]
infos(Noeud n a1 a2) = infos(a1) || [n] || infos(a2)
nbNoeuds :: arbre -> nat
nbNoeuds(Feuille n) = 1
nbNoeuds(Noeud n a1 a2) = nbNoeuds(a1) + nbNoeuds(a2) + 1
Montrez (par induction) que pour tout arbre a, la propriété suivante est satisfaite:
nbNoeuds(a) = length( infos(a) )
Note: Vous pouvez utiliser la propriété suivante (sans la démontrer):
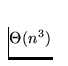 .
. et g est
et g est 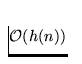 , alors
f est
, alors
f est 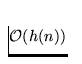 .
.
Algorithme produit( a, b: nat ) prod: nat
prod <-- 0
TANTQUE b > 0 FAIRE
SI b MOD 2 = 1 ALORS
prod <- prod + a
FIN
b <- b / 2
a <- 2 * a
FIN
RETOURNER prod
FIN
Quelle est la complexité asymptotique de cet algorithme? Justifiez.
[9] b) L'algorithme suivant permet de trouver le minimum et le maximum d'une séquence s de nombres naturels (le résultat est une paire de nombres, paire indiquée par ``(min, max)''):
Algorithme min_max( s: sequence{nat} ) (min, max): (nat, nat)
SI length(s) = 1 ALORS
min <- s[0]
max <- s[0]
SINON
(min1, max1) <- min_max( s[0..length(s)/2-1] )
(min2, max2) <- min_max( s[length(s)/2..length(s)-1] )
min <- min1 < min2 ? min1 : min2
max <- max1 > max2 ? max1 : max2
FIN
RETOURNER (min, max)
FIN
Quelques éléments à souligner:
public class C implements T {
private PriorityQueue pq;
private int suivant;
public C() {
pq = new PriorityQueue( new IntegerComparator() );
suivant = 1;
}
public int m1() { return pq.size(); }
public boolean m2() { return pq.isEmpty(); }
public Object m3() throws TException {
try {
return pq.minElement();
}
catch( RuntimeException ce ) {
throw new TException( "??" );
}
}
public void m4( Object element ) {
pq.insertItem( new Integer(suivant), element );
suivant = (suivant % Integer.MAX_VALUE) + 1;
}
public Object m5() throws TException {
if ( ! pq.isEmpty() ) {
return pq.removeMinElement();
} else {
throw new TException( "??" );
}
}
}
private Object trouver( Sequence s, Object k, int low, int high ) {
// On suppose qu'un Comparator c est accessible pour comparer les cles.
if ( low > high )
return NO_SUCH_KEY;
else if ( low == high ) {
Item item = ((Item) s.elemAtRank(low));
return item.key() == k ? item.element() : NO_SUCH_KEY;
} else {
Item iteml = ((Item) s.elemAtRank(low));
Item itemh = ((Item) s.elementAtRank(high));
if ( c.isEqualTo(k, iteml.key()) )
return iteml.element();
if ( c.isEqualTo(k, itemh.key()) )
return itemh.element();
if ( c.isGreaterThan(k, iteml.key()) && c.isLessThan(l, itemh.key()) )
return trouver( s, k, low+1, high-1 );
return NO_SUCH_KEY;
}
}
L'appel initial à cette procédure pour fouiller une séquence s se fait alors comme suit:
return trouver( s, k, 0, s.size()-1 );
Quelle sera la complexité asymptotique de cette méthode (en fonction de la taille de s, qu'on suppose égale à n) si la séquence s est mise en oeuvre avec une liste doublement chaînée plutôt qu'avec un tableau d'items? Justifiez votre réponse.
6. Tas (16 pts) Note: Dans les questions qui suivent, la structure de tas est toujours telle que la clé minimum est conservée à la racine de l'arbre (conceptuellement) associé au tas. [4] a) Dans une structure de tas vue comme un arbre binaire complet partiellement ordonné, que peut-on dire concernant la position dans le tas de la clé la plus grande, en supposant que chaque clé est unique? Expliquez birèvement. [4] b) Dans une structure de tas représentée par un tableau d'items, est-ce qu'un tableau trié en ordre croissant forme effectivement un tas? Expliquez! [8] c) Soit l'algorithme suivant qui calcule la somme des k plus petits éléments de A, un tableau d'entiers naturels:
Algorithme sommePartielle( A: array[1..n] OF nat, k: nat ) somme: nat
DEBUT
construireTas( A ) // Definition omise: cf. plus bas.
somme <- 0
POUR j <- 1 A k FAIRE
somme <- somme + A[1]
echanger A[1] <-> A[n-j+1]
entasser( A, 1, n-j )
FIN
RETOURNER somme
FIN
Algorithme entasser( A: array[1..n] OF nat, i: nat, k: nat )
DEBUT
SI 2*i <= k & A[2*i] < A[i]
ALORS min <- 2*i
SINON min <- i
SI 2*i+1 <= k & A[2*i+1] < A[min]
ALORS min <- 2*i+1
SI min != i
ALORS echanger A[i] <-> A[min]
entasser( A, min, k )
FIN
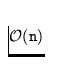 . Quelle sera alors la complexité
asymptotique de l'algorithme sommePartielle, en fonction de
n et k?
. Quelle sera alors la complexité
asymptotique de l'algorithme sommePartielle, en fonction de
n et k?
Supposons alors une classe Arbre définie (partiellement) comme suit:
public class Arbre implements SimpleTree {
private NoeudEF racine;
private int taille;
...
}
Écrivez (en Java) la classe locale permettant, pour un noeud donné, d'énumerer ses enfants. Plus précisément, définissez la classe locale EnumerationChildren dont une instance est créée lors d'un appel à children.
public Enumeration children( Position p ) {
return new EnumerationChildren(p);
}